Difference between revisions of "Turing machine"
(Add category, some external links to toy physical ones, etc) |
m (Bold 'Turing complete' (for use as a target)) |
||
| Line 17: | Line 17: | ||
</blockquote> | </blockquote> | ||
| − | The basic operation is that each square can have a single symbol from a finite | + | The basic operation is that each square can have a single symbol from a finite set of symbols; each step possibly changes the symbol and moves the tape to the left or the right. |
| − | set of symbols; each step possibly changes the symbol and moves the tape to the | ||
| − | left or the right. | ||
They are comprehensively covered in computing literature, with endless variations, including a large number of physical implementations. | They are comprehensively covered in computing literature, with endless variations, including a large number of physical implementations. | ||
| Line 25: | Line 23: | ||
A number of very important theoretical results came from study of these machines: | A number of very important theoretical results came from study of these machines: | ||
| − | * A Turing machine is adequate to simulate any other kind of automata, ignoring specified size and speed constraints. | + | * A Turing machine is adequate to simulate any other kind of [[automata]], ignoring specified size and speed constraints. |
| − | * A machine which can simulate a Turing machine can therefore simulate ''any'' machine and is said to be ''Turing complete''. | + | * A machine which can simulate a Turing machine can therefore simulate ''any'' machine and is said to be '''Turing complete'''. |
{{semi-stub}} | {{semi-stub}} | ||
Latest revision as of 04:21, 10 April 2024
A Turing machine is an abstract computer (ironically, created before the first real computer), devised by mathematician Alan Turing in 1936, to develop theories of computability -- that which can, and which cannot, be computed.
The classic introduction to this kind of machine is MIT professor Marvin Minksy's Computation: Finite and Infinite Machines (Prentice-Hall 1967):
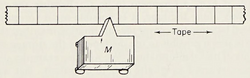
A Turing machine is a finite-state machine associated with an external storage or memory medium. This medium has the form of a sequence of squares, marked of on a linear tape. The machine is couple to the tape through a head, which is situated, at each moment, on some square of the tape (see fig). The head has three functions, all of which are exercised in each operation cycle of the finite-state machine. The functions are: reading the square of the tape being scanned, writing on the scanned square, and moving the machine to an adjacent square (which becomes the scanned square in the next operation cycle).
The basic operation is that each square can have a single symbol from a finite set of symbols; each step possibly changes the symbol and moves the tape to the left or the right.
They are comprehensively covered in computing literature, with endless variations, including a large number of physical implementations.
A number of very important theoretical results came from study of these machines:
- A Turing machine is adequate to simulate any other kind of automata, ignoring specified size and speed constraints.
- A machine which can simulate a Turing machine can therefore simulate any machine and is said to be Turing complete.
See also
External links
- Turing Machines - good lecture notes on the topic, and the environment in which it was create
- A Turing Machine - wonderful site about an actual Turing machine, with a lot of detail
- Lego of Doom - a Turing machine built out of Lego